
It was invented by mathematicians named Rivest, Shamir and Adleman (hence where the name RSA was derived) in year 1978. RSA is a modern cryptographic algorithm that encrypts and decrypts data. RSA is a term quite commonly used when it comes to cryptography.
Now, we’ll extend Fermat’s one to prove Euler’s theorem. We’ve already proven the Fermat’s Little Theorem. Even though, applying the algorithm is very easy, it lies behind powerful math theorems.
Keys in the RSA Algorithm are not the regular steel or aluminum ones we know about. That simply means it uses a public key as well as a private key. Swiss Mathematician Leonhard Euler Fermat’s Little TheoremRSA is an encryption algorithm that falls in the class of being an asymmetric encryption algorithm.

However, we will define n as multiplication of two primes.We’ll turn back to Fermat-Euler generalization. Totient function still means number of integers between 1 and n that are coprime to n. It says any module n, and any integer a coprime to n. In this case, totient must be n-1.In Euler’s statement, n does not have to be prime. Notice that n is a prime number in Fermat’s Little Theorem.
Is it familiar?Yes, it is Fermat-Euler generalization. M mod nNow, please focus on the term in the parenthesis. Let’s calculate m to e to d.(m e) d mod n = m e d mod n = m k. ϕ(n) + 1Suppose that m is the message. Then, we’ll find its multiplicative inverse for module ϕ(n) and named it d.We can express this term as e.d = k. The question is that what is ϕ(n) or ϕ(pq) because it is not prime.Herein, totient function is a multiplicative function. This property is based on Chinese Remainder Theorem.That is why, we can produce a generalized demonstration.Then, the algorithm instructs to pick a random number e that co-prime to ϕ(n).
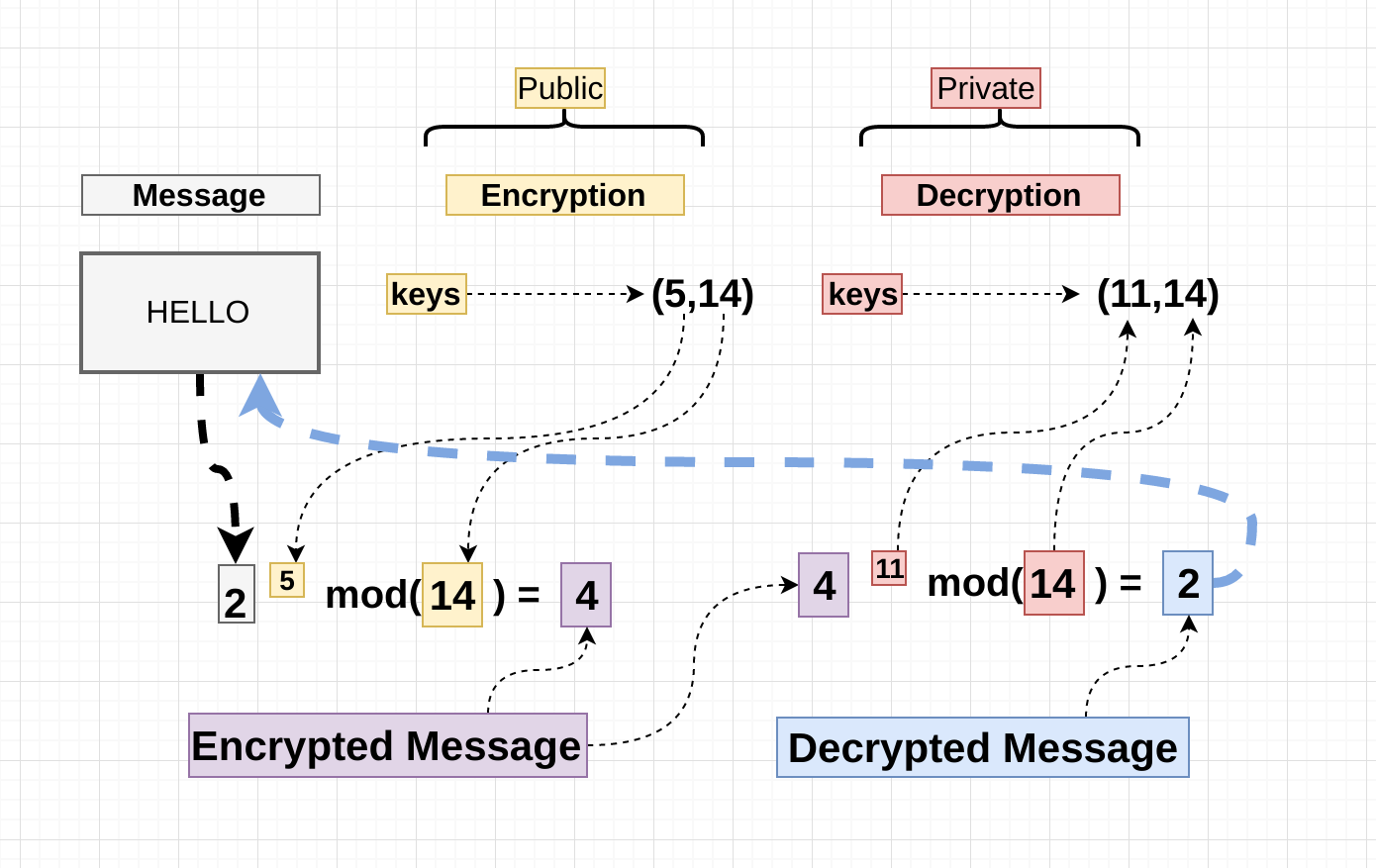
Even the physics could change, consider Galileo’s physics and Einstein’s physics. On the other hand, all other sciences would change. This is the satisfactory part of math, it does not change. However, we’ve just put these genius mathematicians’ discoveries in backbones of security world in 21th century. Interestingly, Fermat lived in 17th century and Euler lived in 18th century. Today, most of digital signatures and certificates are launched on this algorithm.


 0 kommentar(er)
0 kommentar(er)
